This  strategy task is to estimate the water losses due to evaporation. It is based on the approach proposed by Ritchie (1972), and on the implementation of this algorithm in the WEPP model (Flanagan and Nearing, 1995). This implementation is characterized by an adaptation to a layered soil. Evaporation, the maximum soil evaporation effective depth, and the total soil evaporation values are provided as outputs layer by layer.

 

This model calculates the bare soil evaporation, Esb, in two stages.

In the first stage, soil evaporation is limited only by the energy available at the soil surface and, therefore, it is equal to potential soil evaporation, Esp.

The upper limit for the stage one soil evaporation is calculated as follows:

 

  

 

where Esu is the upper limit soil evaporation of stage one (m), and Tr is the soil transmissivity (mm d−0.5 ), dependent on soil texture calculated as an average among layers between surface to 13 cm, and computed as:

 

 

where Sa and Cl   are respectively sand and clay percentages in the bare soil evaporating layer.

 

When the accumulated soil evaporation exceeds the stage one upper limit, Esu, stage two evaporation starts to be computed.

 

Stage two soil evaporation is estimated by the following equation:

 

 

where S2 is the stage two bare soil evaporation rate for a day (m d−1) and d2 is DOY (day of the year) since stage two soil evaporation starts.

 

When precipitation value is higher than or equal to accumulated stage two soil evaporation value, then stage one

soil evaporation is assumed.

 

During a drying cycle, evaporation from the soil continues until the soil water content reaches a one third of wilting point value, a moisture content below whose no more water can evaporate from the bare soil.

 

Computed bare soil evaporation, Esb, in either stage is reduced with increased plant residue using the equation taken from the WEPP model, chapter 5 (Savabi and Williams, 1995) based on a personal communication by J.L.Steiner:

 

 

where Eact is the actual soil evaporation (m d−1), Esb is the bare soil evaporation (m d−1), and C is the plant residue on soil (kg ha−1). 

 

Calculation of evaporation depth

 

1. calculation of the maximum evaporation depth. The maximum evaporation depth Devmax (m)  is a function of soil texture, and computed as follows:

 

 

2.  calculation of the evaporation depth D evap (m):

 

 

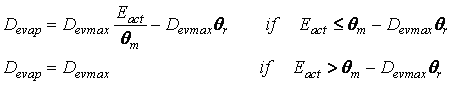
θm is above Devmax soil layers water content (m), θr is the residual soil water content (m3 m-3).

When soil water content soil value is lower than Eact value (calculated at the depth Devap), all the water available up to the θr is assumed to be evaporated.

When soil texture and water content values are constant all along soil profile, the evaporation output (mm) is provided for each layer, assuming evaporation to be uniform along the estimated evaporation depth.

 

Adaptation to layered soil

When soil layers' characteristics are not homogeneous, an approximate procedure is developed here, based on averaging soil characteristics and soil water content. When silt and clay content are not homogenous in the first 0.13 m of soil, an approximate procedure to estimate transmissivity is adopted, assuming the maximum possible depth of evaporation to be equal to the one of a most sandy layer. There is no test of method for obtaining transmissivity in layered soil, but the most common condition in agricultural soil is the homogeneity of surface layer texture, due to tillage operation. In no-tillage system, probably, this approach is not well suitable due to the differences, in the very first layers, of the organic matter content. Details follow:

1) computation of transmissivity for each layer constituting the soil profile (till to maximum depth of 0.13 mm, because an evaporation depth higher 0.13 m is never allowed with the Ritchie approach);

2) detecting highest transmissivity value among whom computed;

3) calculation of Eact using transmissivity as initial guess approximation;

4) Computing Devmax in function of the maximum evaporation depth and a weighted average of textures;

5) Computation of Devap using the highest transmissivity computed value as initial guess approximation, and a weighted average among layer of   θr;

6) Calculating Eact, only for above the Devap just computed layers;

7) Partitioning of Devap among layers proportionally to  available water content (=SWC-θr).

Created with the Personal Edition of HelpNDoc: Easy to use tool to create HTML Help files and Help web sites